本期,我们将介绍谐振转换器同步整流器 (SR)设计注意事项。
谐振转换器的运行状态比脉宽调制转换器的运行状态复杂得多。以图 1中的电感-电感-电容-串联谐振转换器 (LLC-SRC) 为例,在给定的负载条件以及开关频率 (fsw) 相对位置和串联谐振频率 (fr) 下,常规 LLC-SRC 设计中有四种常见状态(图 2)。在 fswr 时,整流二极管电流在有源开关 (Q1 或 Q2) 关断前变为零。因此,将金属氧化物半导体场效应晶体管 (MOSFET) 用作整流器(即 SR)时,SR 必须关断且占空比小于 50%,以免整流器电流回流。否则,过大的循环电流会影响转换器效率。
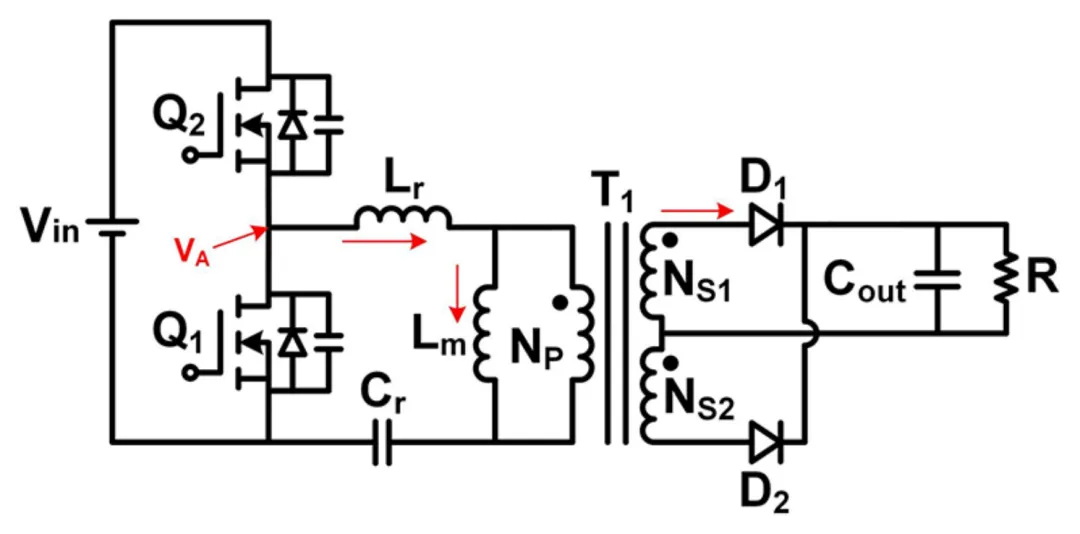
图 1:电感-电容串联谐振转换器 (LLC-SRC) 提供了软开关特性,允许高频运行
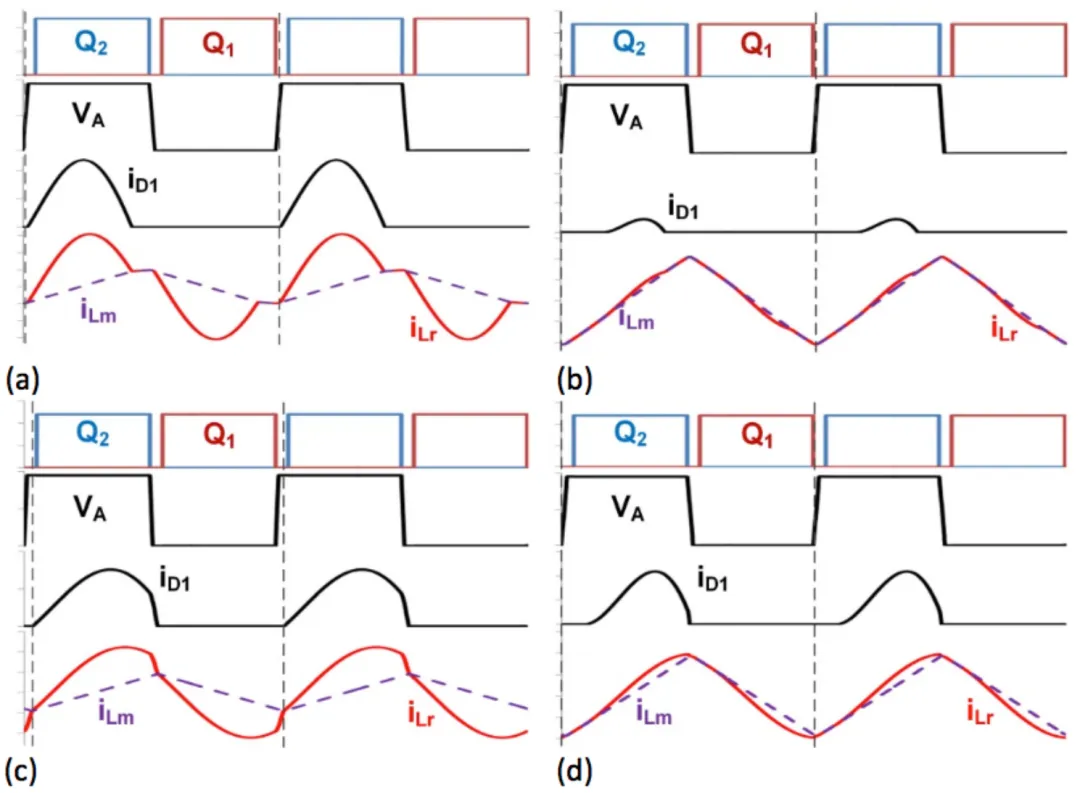
图 2:在重负载和 fswr(a)、轻负载和 fswr(b)、重负载和 fsw>fr(c) 以及轻负载和 fsw>fr(d) 条件下的 LLC-SRC 运行状态表明,在施加 SR 的情况下,需要进行电流检测,以免输出整流器上出现反向电流
在 fswr 时,重负载下的整流器电流传导时间实际上为 0.5/fr。因此,在 fswr 时,可以将重负载下的 SR 导通时间限制为略小于 0.5/fr,并在较轻负载下禁用 SR。但是,这种开环 SR 控制方法无法优化转换器效率。 更可靠的 SR 控制方法是通过 MOSFET 漏源电压 (VDS) 检测(图 3)。基本上,此 SR 控制方法会将 MOSFET VDS 与两个不同的电压阈值进行比较,以导通和关断 MOSFET。一些较新的 VDS 检测 SR 控制器(例如德州仪器 (TI) 的 UCC24624)甚至还有第三个电压阈值来激活比例栅极驱动器,从而以极小的延迟快速关闭 SR。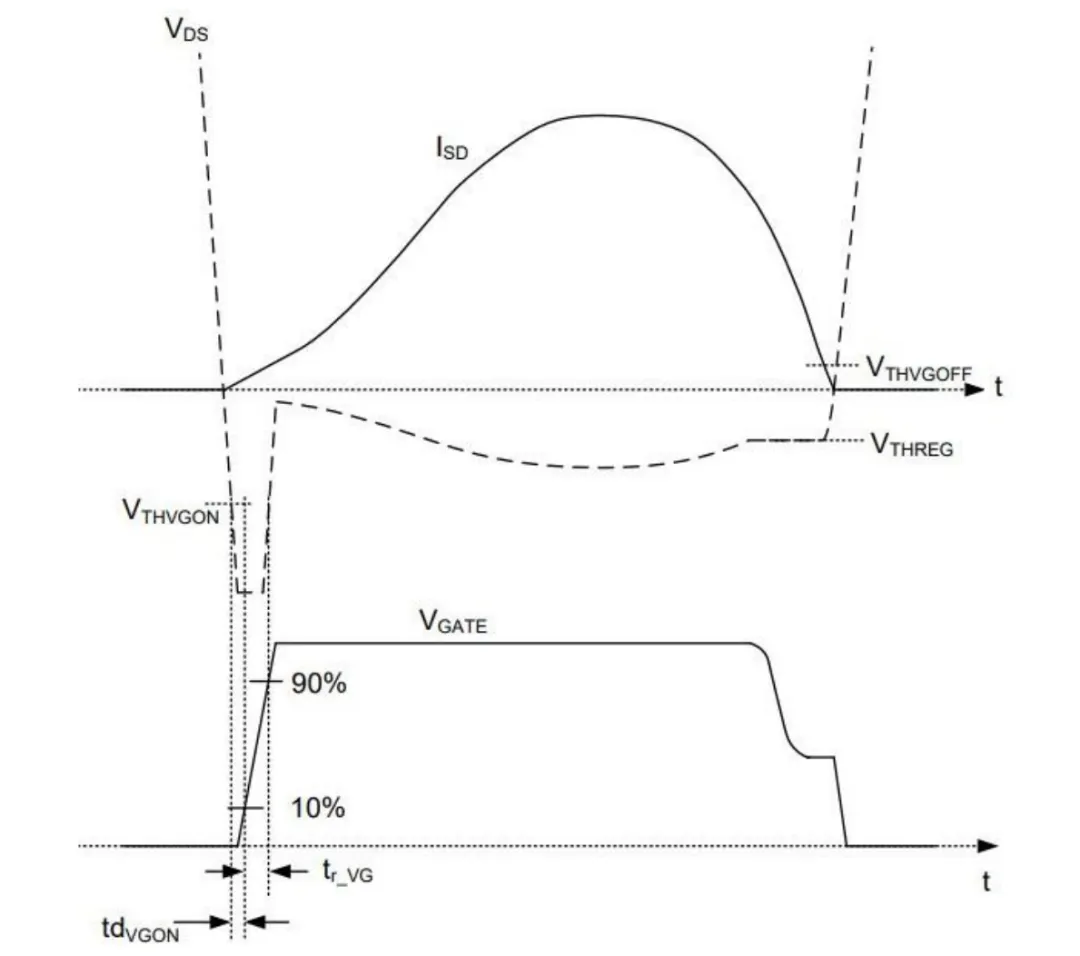
图 3:VDS 检测 SR 会在不同的 VDS 电压电平下打开和关闭 SR
值得注意的是,电压阈值均为毫伏级;需要高精度检测电路。因此,VDS 检测方法通常通过使用集成电路来实现,集成电路具有 VDS 电平(通常小于 200V)和 fsw 限制(通常小于 400kHz)。由于 VDS 检测 SR 控制方法存在局限性,您将需要使用不同的 SR 控制方法来优化高压和高频谐振转换器的 SR 导通。 在 Rogowski 线圈后面使用积分器和比较器是控制高频谐振转换器 SR 的另一种方法。图 4 方框图展示了在电容-电感-电感-电感-电容串联谐振双有源电桥转换器 (CLLLC-SRes-DAB) 上使用 Rogowski 线圈进行 SR 控制。带绕组的空芯线圈(Rogowski 线圈)放置在变压器绕组上,用于电流检测。当时变电流流经线圈时,电流生成的磁通量会在线圈绕组上感应出电压。与原始时变电流相比,感应电压将具有 90 度的相位差。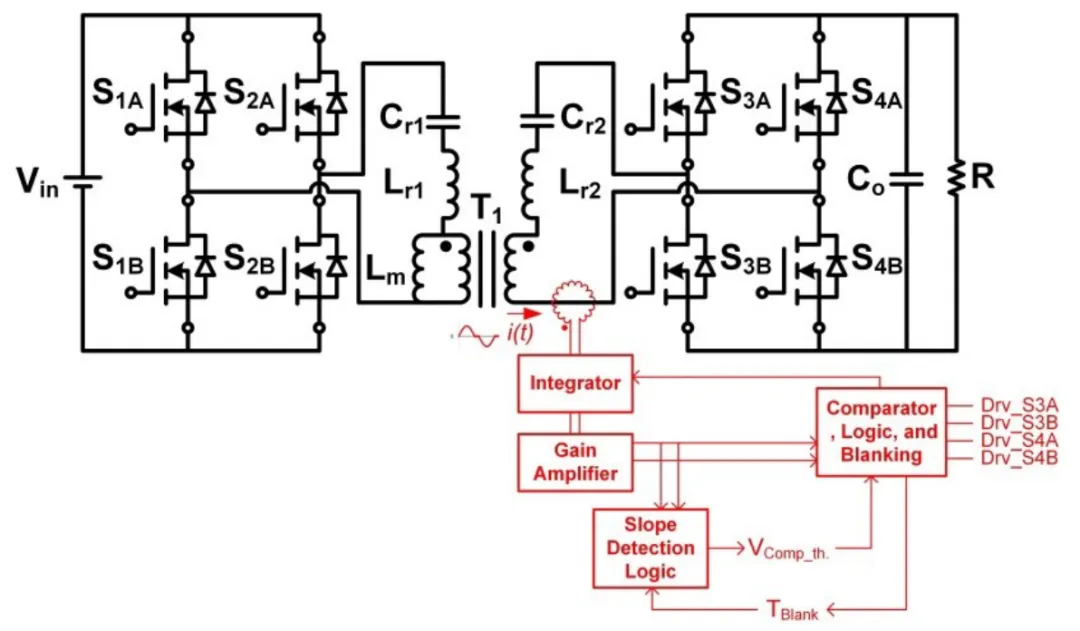
图 4:Rogowski 线圈 SR 控制可在 CLLLC-SRes-DAB 转换器中实现精确的高频 SR 感应和控制
在 Rogowski 线圈之后添加积分器,可以产生同相电压,甚至超前原始时变电流。因此,可以将积分器输出的电压过零点设置为略早于时变电流的过零点,以适应可能的传播和控制延迟。然后将放大的积分器输出信号与给定的比较器阈值进行比较,以生成具有近乎优化的 SR 导通时间的 SR 驱动信号。在控制电路中插入的额外斜率检测逻辑可在不同负载条件下进一步优化 SR 传导时间。由于 Rogowski 线圈通过磁通量检测电流,因此不存在电压电平限制。此外,Rogowski 线圈使用空芯而不是磁芯材料,因此其带宽非常高且没有饱和限制;因此,与 VDS 检测 SR 控制方法不同,即使在兆赫级谐振转换器上也没有频率限制问题。 图 5 说明了此处建议的方法。将图 5 中的时变电流定义为 i(t),并假设 Rogowski 线圈垂直放置在变压器绕组上,可以使用方程式 1 来计算 Rogowski 线圈绕组输出电压,如下所示: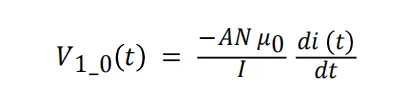
方程式 1
其中,A 是 Rogowski 线圈上每匝的横截面面积(假设 Rogowski 线圈上的各匝都具有相同的横截面面积),N 是 Rogowski 线圈上的匝数,l 是 Rogowski 线圈的周长,μ0 = 4π · 10-7H/m 是磁导率。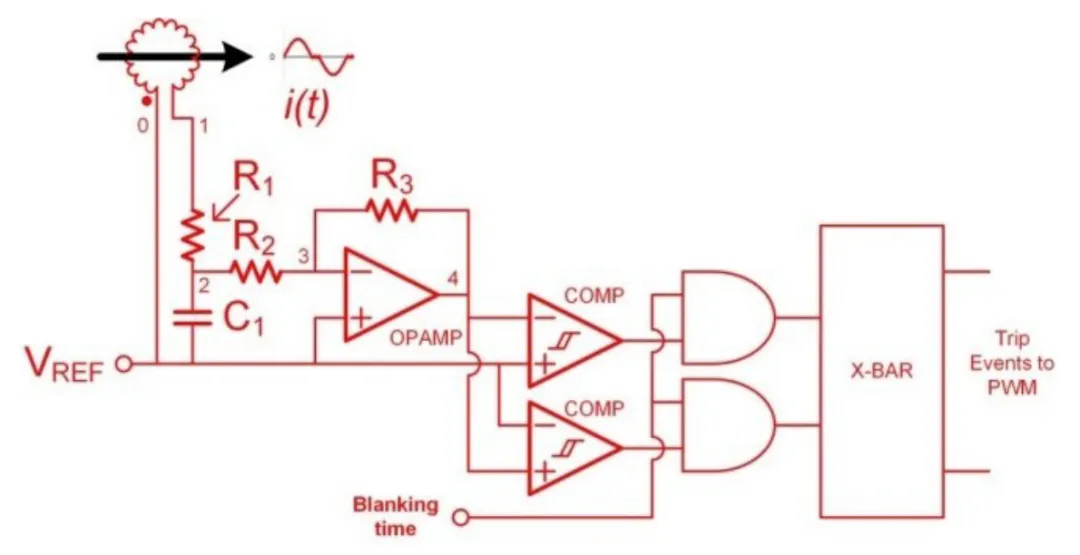
图 5:无源积分器允许 Rogowski 线圈 SR 控制电路预测电流过零点时序
假设在建议的感应电路中使用理想的运算放大器,方程式 2 这样表示 Rogowski 线圈输出 v1_0 与无源积分器输出 v2_0 之间的电压关系: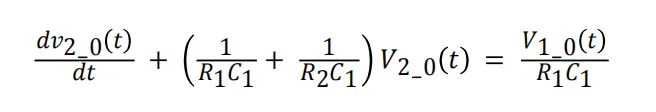
方程式 2
可使用方程式 3 形式求解方程式 2 中的差分方程: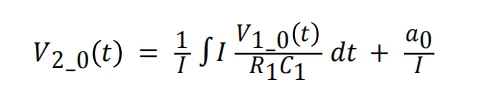
方程式 3
其中 a0 是一个常量,用方程式 4 表示。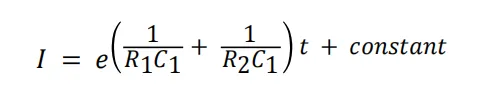
方程式 4
为了更轻松地了解如何调整无源积分器和放大器的相位差,假设时变电流是纯正弦,这将使 Rogowski 线圈输出电压和积分器输出为纯正弦。换言之,求解方程式 1 和方程式 2 得到 i(t) 的解,假设 v2_0(t) = a1sin(ωt),方程式 2 可以重写为方程式 5: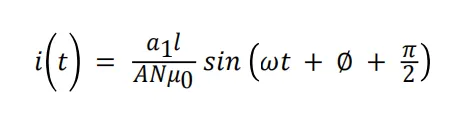
方程式 5
其中,方程式 6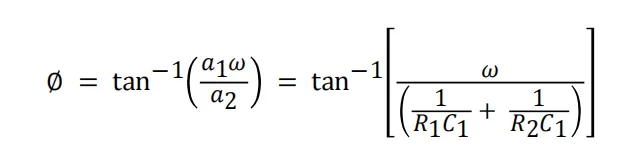
方程式 6
翻转 Rogowski 线圈的引脚排列,时变电流变为方程式 7: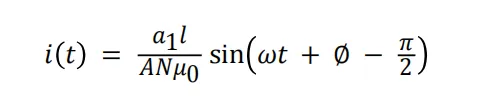
方程式7
当在方程式 3 中将 Φ 设为 −π/2、在方程式 4 中将 Φ 设为 π/2 时,通过在 Rogowski 线圈输出和积分器输入之间使用正确的连接极性改变 R1、R2、C1 和 fsw(ω = 2πfsw) 的值,积分器输出 v2_0(t) 可以与 SR 电流 i(t) 同相。此外,在实际应用中,可以设置积分器波形以引导 SR 电流。因此,在控制器和驱动器分别有响应时间和传播延迟的情况下,SR 关断时序仍能达到零电流电流过零点。 图 6 展示了检测电路的绕组电流测量值和增益放大器输出电压。如您所见,将零电压电流过零点编程为比实际检测电流更早关断,可以调节传播和控制延迟。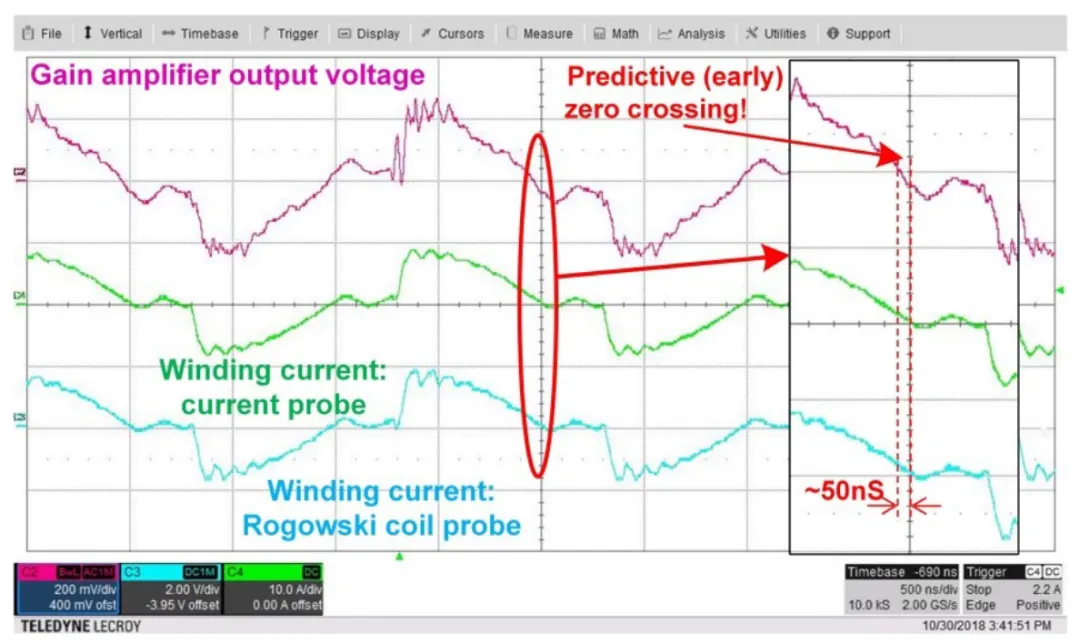
图 6:此 SR 电流测量比较展示了预测性 SR 感应,即积分器输出的电流过零点早于实际的电流过零点
图 7 所示为开关频率低于串联谐振频率时的理想 SR 关断时序。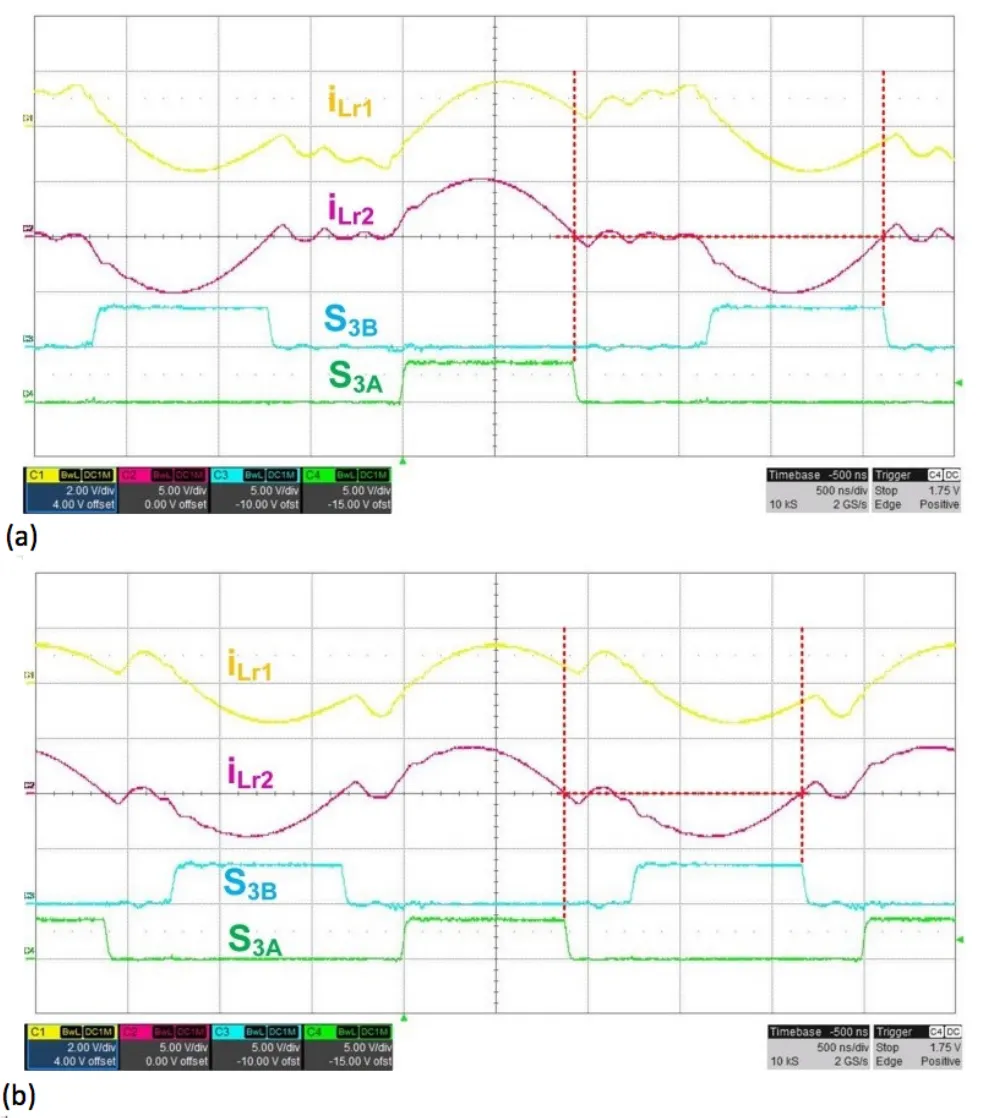
图 7:在 300kHz(a) 和 400kHz(b) 下,SR 在理想的电流过零点关断
文章来源:德州仪器
