公众号 | 高速先生
作者 | 姜杰
聊电容,不能只聊电容,还要聊电阻和电感。
看似很简单,其实,一点都不难。
因为去耦电容的模型基本都可以用下面三种元素的简单组合来表示。

理想电容C的阻抗是随频率的增加而逐渐减小的一条斜线,实际上由于电容中等效寄生电阻(ESR)和等效寄生电感(ESL)的搅局,问题开始变得复杂。不同的电容自谐振频点不同,谐振点阻抗各异,滤波频段也有区别……
看似很复杂,其实,很简单。
电容搞搞“振”,第一“振”来自同一电容ESR\ESL\C的串联谐振(也叫做自谐振)。

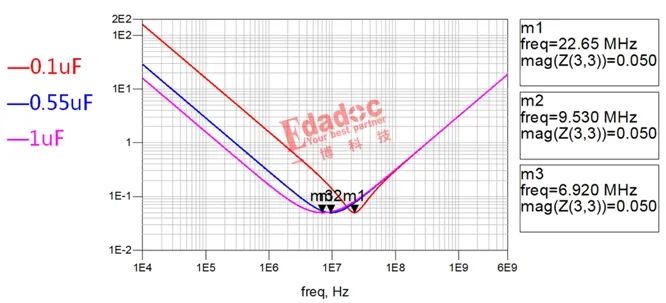
先来看看电容模型的各参数是如何影响阻抗曲线的。对于电容容值C,不难发现,相同ESR和ESL的情况下,随着容值的增加,自谐振频点向低频移动,同时,滤波频段也会加宽。
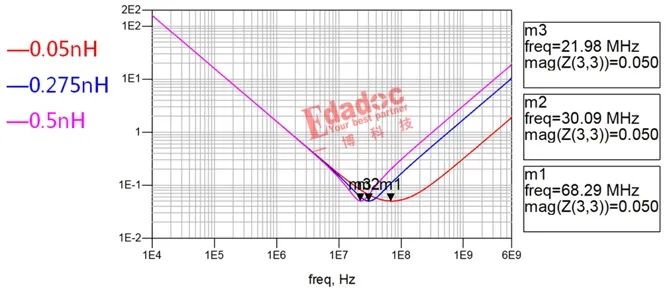
接下来再看哈ESL的影响。在保持其它参数不变的情况下,随着ESL的增加,自谐振频点向低频移动,同时,滤波频段也会随着变小。
需要注意的是,ESR的情况会复杂一些,因为它是一个频变的参数。
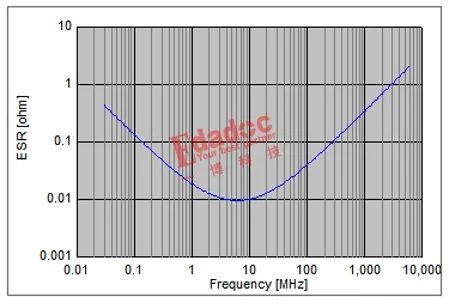
ESR随频率变化的趋势与该电容的阻抗变化一致。
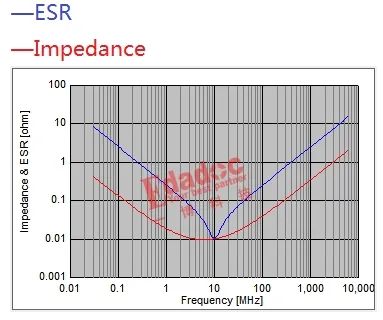
不过,为了简化问题,我们这里先把ESR作为一个常数,它的变化对阻抗曲线的影响如下图:
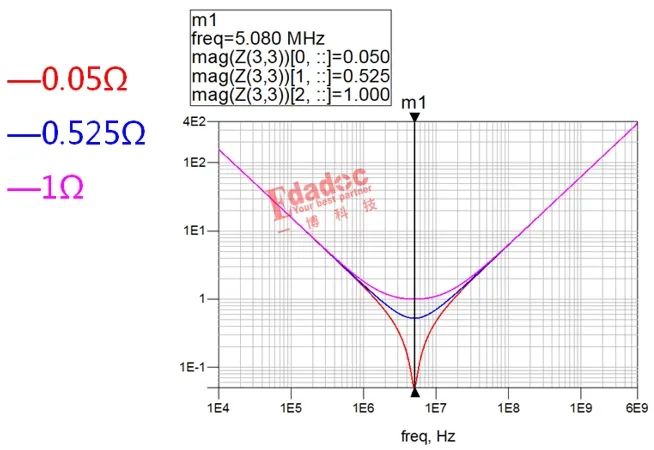
对比上面几个图,我们会发现一个有趣的现象,那就是电容自谐振频点的ESR基本决定了阻抗的最小值。

以上只是单一容值电容的阻抗曲线。了解PDN阻抗曲线的童鞋会发现常见情况并非如此,而是像人生一样总是起起伏伏。

其实,这是容值不同的电容并联谐振的结果,也是本文要说的第二“振”。
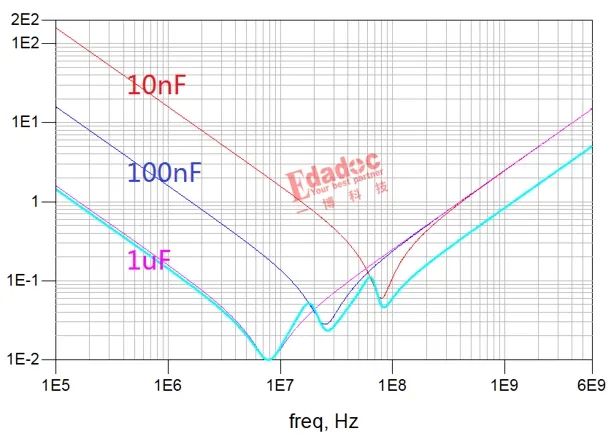
分析起来也很简单,当一个电容的感性区遇上另一个电容的容性区,谐振峰就出现了。

综合考虑VRM和芯片内去耦,如果说第一“振”决定了阻抗曲线的波谷,第二“振”通常确定了阻抗曲线的波峰。
电容种类这么多,原理图设计或者备料出错的机会大大增加,作为一名设计攻城狮,希望板子简单点,精简一些电容,这个要求并不过分吧?
说干就干,在前文三种电容并联的基础上,去掉100nF的电容,看看会怎样。
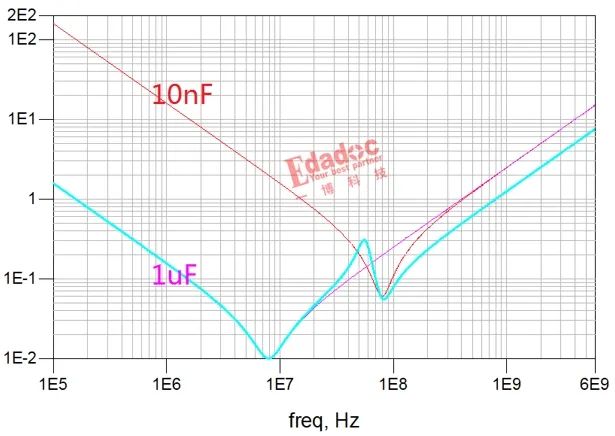
这么看,除了在100nF的去耦频段出现一个谐振峰,好像也没什么问题,毕竟,这个峰值也没那么高。我们继续把VRM和芯片内去耦模型加上,看全链路的情况。
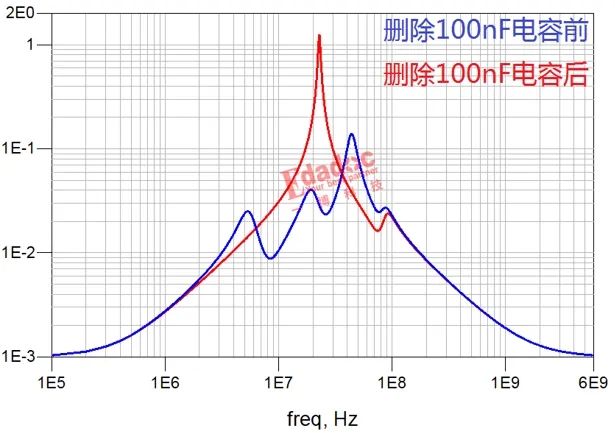
See?高速先生一直强调的调整电容要合理真不是吓唬你。
当然,这个例子只是为了凸显电容影响而挑选的极端情况。
电容不是老虎屁股,一点摸不得,具体种类和数量可以通过仿真进行优化,是增是减,It depends!
本文转载自:高速先生微信公众号
