数字电位器能否代替电路中的机械电位器？

作者：Stephen Woodward，文章来源：EDN电子技术设计

不久前，我发表了一个设计实例“仅需一个电位器，就能将运算放大器增益从-30dB调整到+60dB”。

图1显示了该电路。

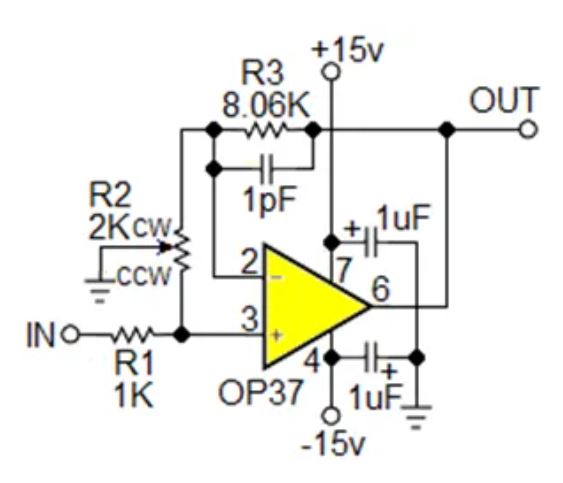
Gain = (R2ccw/(R1 + R2ccw))(R3/R2cw + 1)

图1：接地的电位器使R2同时用作输入衰减器和输出增益调节器。

最近我开始琢磨数字电位器(Dpot)是否可以代替图1中的机械R2。图2显示了一种看似可能的Dpot拓扑。

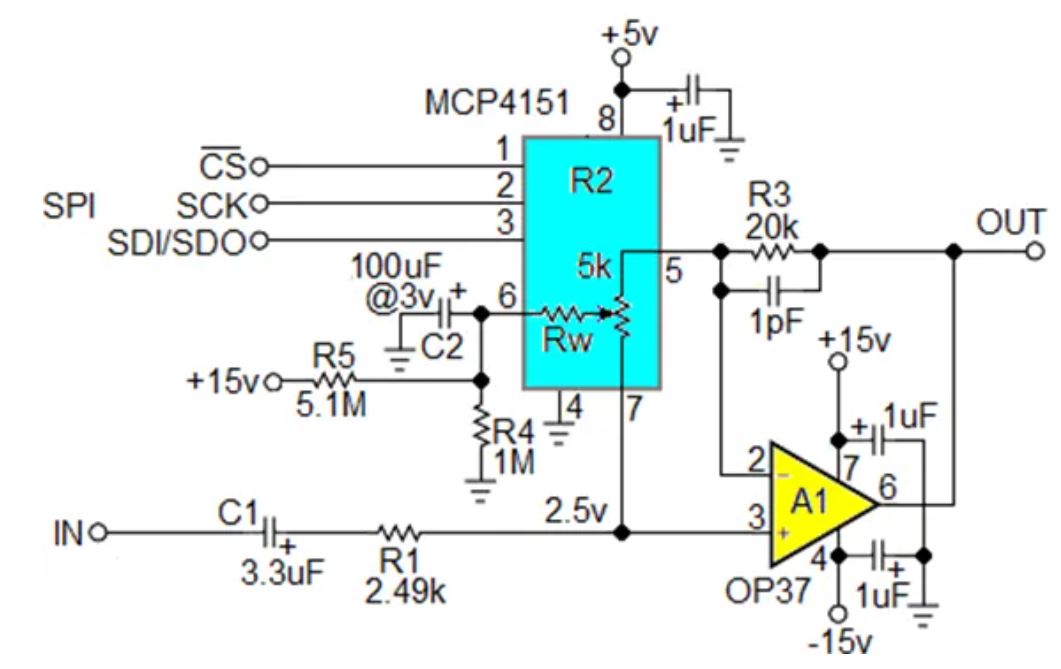
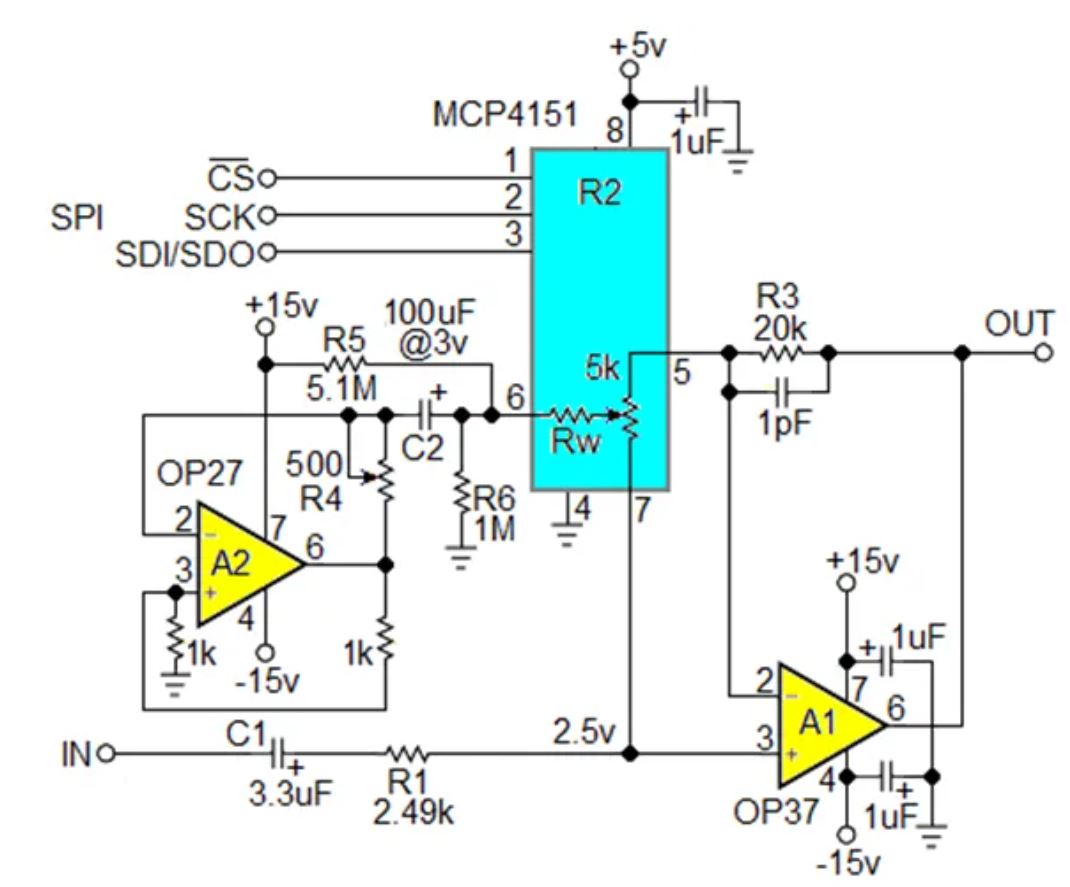
图2：R2的功能与图1相同，但R4 R5 C2提供直流偏置，以适应双极性信号。那么Rw滑动电阻效应如何？

仔细检查后，发现效果并不理想。这是因为滑动电阻干扰了R2两半的隔离，而最初的电路正是通过这种隔离实现工作的。图3显示了我最终采取的解决方案。

图3：将围绕A2的正反馈回路和负反馈回路结合起来，产生有源负阻=-R4。

A2及其周围的网络是这一设计的基础。它们产生有源负阻效应，从Rw中减去，如果调整为R4=Rw，理论上(工程师最不喜欢的词)可以完全抵消它。

一个快速消除Rw的方法是将Dpot设置写为零，提供~1v rms输入，然后修整R4以使输出为零。

以下是一些负阻计算。注意Vp#=A2引脚#处的电压信号。
    令Iw=滑动电阻信号电流，则
    Vp6 = Vp2 – R4*Iw
    Vp2 = Vp3 (negative feedback)
    Vp3 = Vp6/2 (positive feedback)
    Vp6 = Vp6/2 – R4*Iw
    Vp6 – Vp6/2 = Vp6/2 = -R4*Iw
    Vp6 = -2*R4*Iw
    If R4 = Rw, then IR4 = IRw
    -2*R4*Iw = -(R4 + Rw)Iw
    Vw = Vp6 + (Iw*R4 + Iw*Rw) = -Iw(R4 + Rw) + Iw(R4 + Rw)
    Vw = 0 (Rw已被抵消！)

Gain = (R2ds/(R1 + R2ds))(R3/(R2(1 – ds)) + 1)

图4中的红色曲线将图2中的行为与(未补偿)Rw=150Ω(对于图示的Microchip Dpot来说是合理的)进行比较，而黑色曲线显示了当R4=Rw=150Ω时发生的情况。将其与使用机械电位器的原始(图1)电路的性能进行比较，如图5所示。

当然，在Dpot的整个设置范围内，Rw消除的完美程度并不比R5R6提供的2.5v DC偏置下Dpot的257个不同抽头上的Rw匹配更好。给定电位器的电阻阵列内的典型匹配看起来不错，但制造商并没有承诺这些，制造商只承诺了+/-20%左右的系数。不过，将Rw降低到五分之一仍然有用。

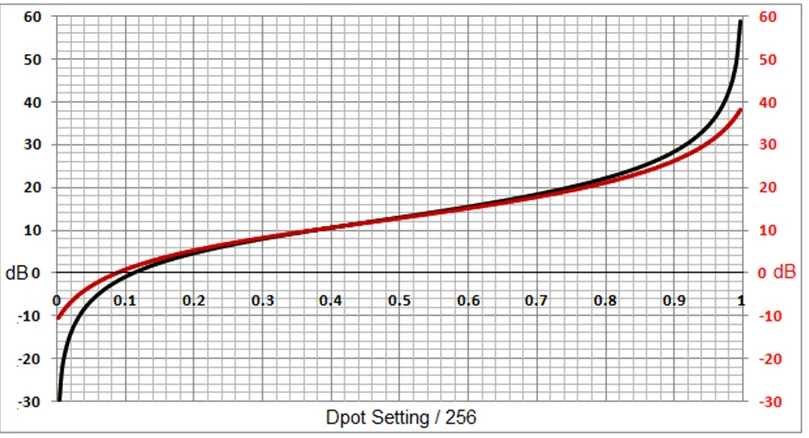
图4：红色曲线表示未补偿的Rw(~150Ω)，请注意跨度两端的20dB损耗。黑色曲线表示用负电阻补偿Rw的情况(R4=Rw=150)。

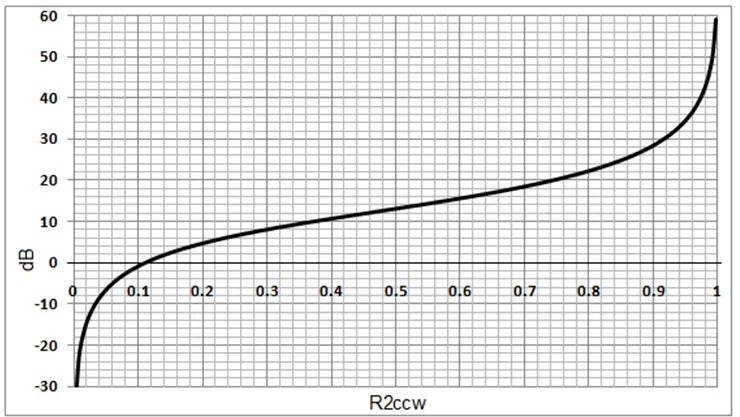
图5：使用机械电位器的增益曲线与带有负电阻Rw补偿的Dpot相同。

注：在发表该实例的机械电位器版本之后，我了解到T.Frank Ritter先生早在50多年前就在其著作“用一个电位器控制运算放大器增益”中提出了该想法，该文发表于1972年麦格劳-希尔出版公司出版的《电子设计师案例手册》上。

因此，我在此向Ritter先生致以迟来的热情敬意。我一直很钦佩先驱者！

(原文刊登于EDN美国版，参考链接：Digital pot can control gain over a 90 dB span like an electromechanical，由Ricardo Xie编译)